Gyllene snittet

Av Ingemar Edfalk

Gyllene snittet är ett sätt att dela in en sträcka eller en yta i harmoniska proportioner. Konstnärer har ända sedan antiken utnyttjat gyllene snittet i bildbyggnaden, För att dela en sträcka enligt gyllene snittet gör man som följer. Om vi kallar sträckan ABC där AC är hela sträckan och B är en punkt någonstans längs sträckan, ska sträckan BC förhålla sig till AB som AB förhåller sig till AC. Alltså: BC/AB = AB/AC. Ett enklare sätt, (tycker jag som är dålig på matamatik), är att istället använda passare och linjal och rita upp delningen såhär:

Dela AC på mitten (B). Rita upp sträckan CD vinkelrätt mot AC. CD ska vara lika lång som halva AC. Förbind A och D med en rät linje. Sätt passarens nål i D och rita från C mot AD tills AD skärs i punkten E. Sätt passarens nål i A och rita från E ner tills sträckan AC skärs. Där har du det gyllene snittet.

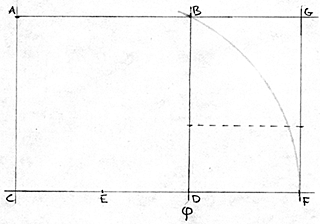
Gyllene rektangeln. Ett annat sätt att jobba med gyllene snittet är utifrån en s.k. gyllene rektangel. Rita såhär:

ABCD är en kvadrat. Dela sträckan CD på hälften så får du punkten E. Sätt passarens nål i E och rita ner från B tills CD:s förlängning skärs i punkten F. AGCF är nu en gyllene rektangel. Det gyllene snittet ligger i punkten D. Man kan sedan fortsätta att rita gyllene rektanglar inuti varandra som ryska dockor. Se den sträckade linjen. Detta var den första artikeln om proportionsförhållanden. Flera följer.